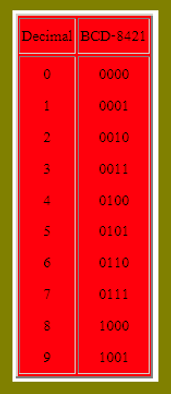
จากตาราง
จะเห็นว่า เลข Decimal 1 Digit เขียนแทนด้วยเลข Binary 4 bits โดยที่แต่ละ bit ของรหัส BCD-8421 ได้กำหนดน้ำหนักไว้ต่างกันคือ bit ทางขวามือมีน้ำหนักเป็น 1,2,4,8 ดังตัวอย่าง เช่น
ตัวอย่าง : เปลี่ยน 576310 ให้เป็นรหัส BCD
576310 = 0101 0111 0110 0011
หมายเหตุ : จะแทนเลขฐานสิบแต่ละหลักด้วยเลขฐานสอง 4 bit
รหัสเกิน 3 (Excess-3 code)
รหัสเกิน3 ดัดแปลงมาจาก BCD-8421 code เมื่อเปรียบเทียบรหัสเกิน3 กับรหัส BCD-8421 จะเห็นว่า Excess-3 code จะมีค่ามากกว่า BCD-8421 code อยู่ 3 หลัก1 ดังตารางข้างล่าง


การเขียนรหัสเกิน 3
แทนเลขฐานสิบสามารถเขียนได้เหมือนกับการเขียนรหัส BCD-8421 แทนเลขฐานสิบ เมื่อนำรหัสเกิน 3 มาเขียนแทนเลขฐานสิบ จะสามารถเขียนแทนเลขฐานสิบได้ในแต่ละหลักด้วยรหัสเกิน 3 จำนวน 4 หลัก หรือ 4 บิต ดังนั้นถ้าเขียนแทนเลขฐานสิบมากกว่าหนึ่งหลักก็จะเขียนด้วยรหัสเกิน 3 เป็นชุด ๆโดยมีรหัสเกิน 3 ชุดละ 4 บิต แสดงการเปรียบเทียบรหัสเกิน 3 กับรหัส BCD-8421ดังตัวอย่าง เช่น
ตัวอย่าง จงเปลี่ยน 5610 ให้เป็น Excess – 3
0101 0110 (BCD)
0011 0011 (บวก 3 แต่ละหลัก)
1000 1001 (Excess 3 code ของ 5610)
การแปลงเลข Binary ให้เป็น Gray code
มีขั้นตอนการแปลงเลขฐานสอง เป็น รหัสเกรย์ดังนี้
1. เริ่มจากบิตแรกซึ่งถือว่ามีนัยสำคัญมากที่สุด (MSB) ดีงมาไว้เป็นบิตแรกเช่นเดิม
2. นำบิตแรกไปบวกกับบิตตัวที่ 2
3. นำบิตตัวที่ 2 ไปบวกกับบิตตัวที่ 3
4. นำบิตตัวที่ 3 ไปบวกกับบิตตัวที่ 4 ไปเรื่อยๆจนหมด ผลบวกที่เราได้ ก็คือ Gray Code เช่น


การแปลงเลข Gray code ให้เป็น Binary
ขั้นตอนการแปลงจากรหัสเกรย์ เป็นเลขฐานสอง
1. เริ่มต้นจากบิตซ้ายมือสุด หรือบิตที่มีนัยสำคัญมากที่สุด ของรหัสเกรย์ ดึงบิตนี้ไปเขียนเป็นรหัสเลขฐานสอง ค่าตัวเลขเหมือนกับรหัสเกรย์
2. นำ MSB ของเลข Binary บวกกับ bit ที่2 จาก MSB ของรหัสเกรย์ใช้หลักการบวกเช่นเดียวกับการเปลี่ยนเลขฐานสองเป็นรหัสเกรย์ ผลบวกที่ได้คือบิตที่ 2จาก MSB ของเลขฐานสอง
3. นำบิตที่ 2 จาก MSB ของเลขฐานสองบวกกับบิตที่ 3 จาก MSB ของรหัสเกรย์ ผลบวกที่ได้คือบิตที่ 3 จาก MSB ของเลขฐานสอง การบวกกันจะทำเช่นนี้ไปเรื่อย ๆ ก็จะได้ผลลัฑธ์เป็นเลขฐานสองเช่น


รหัสASCLL รหัสที่กล่าวมาแล้วทั้งหมดเป็นรหัสเลขฐานสองที่ใช้แทนตัวเลข 0 ถึง 9 แต่ยังมีรหัสเลขฐานสองอีกลุ่มหนึ่งที่ใช้แทนอักขระทั้งตัวอักษร ตัวเลข และสัญลักษณ์พิเศษ เราเรียกว่า Alphanumeric Code ในปัจจุบันมีรหัสมาตรฐานที่ใช้กันอยู่ 2 อย่าง ได้แก่ EBCDID (Exented BCD Interchange Code) และASCII Code (American Standard Code for Informatiom Interchange) ดังได้กล่าวนำแล้ว สำหรับเนื้อหาในบทนี้จะขอกล่าวเฉพาะรหัส ASCII Code ซึ่งเป็นรหัสที่ใช้กันมากและเป็นมาตรฐานของ PC ในปัจจุบัน
ASCII Code เป็นรหัสที่ถูกพัฒนาจนเป็นที่ยอมรับให้เป็นมาตรฐานของรหัสที่ใช้ในคอมพิวเตอร์ เป็นรหัสขนาด 7 บิท สามารถใช้แทนอักขระและรหัสควบคุมต่างได้ ถึง 128 รหัส (0-127, 72=128) ซึ่งสามารถใช้แทนอักษรภาษาอังกฤษตัวเล็ก ตัวใหญ่ ตัวเลข 0-9 เครื่องหมายอักขระพิเศษ และรหัสควบคุมอีก 32 รหัส นอกจากนี้ยังเพิ่มรหัสส่วนขยายอีกโดยเพิ่มเป็นรหัส 8 บิท จึงมีส่วนขยายเพิ่มเติมตั้งแต่ 128 – 255 เพื่อใช้แทนกราฟิก สัญลักษณ์ทางคณิตศาสตร์ และเหลือรหัสเพียงพอที่จะใช้แทนอักขระภาษาต่างประเทศอื่น ๆ อีก เช่นภาษาไทย เป็นต้น